Збірник наукових статей

Завжди було прийнято вважати, що знання логіки є обов'язковим для освіченої людини. Нині, за умов корінного зміни характеру людської праці, цінність такого значення зростає. Свідчення тому - значення комп'ютерної грамотності, однією з теоретичних основ є логіка.

Знання логіки та вміння застосовувати її до вирішення завдань підвищує культуру мислення, виробляє навичку мислити грамотно, розвиває критичне ставлення до своїх та чужих думок.

Завдання, які ми розібрали, пов'язані зі звичайною діяльністю мислення. Ці завдання покликані як оживити виклад, а й наочно продемонструвати, що логічне - це предмет спеціальних роздумів, а й те, із чим постійно стикається кожен. Крім того, приклади дозволяють показати, що реальне мислення не зводиться до логічної послідовності. В процесі завдань важливим виявляється, як правило, все: і послідовність, і інтуїція, і емоції, і образне бачення світу і багато іншого.

Існують різні способи формалізації, як умов завдання, так і процесу її розв'язання: алгебраїчний, табличний, графічний та ін. Кожен із цих способів має свої переваги.

Так, наприклад, при застосуванні методу алгебри найбільш важким є переклад тексту завдання на мову формул. Далі, якщо ви знаєте, логічні закони та правила спрощення виразів, розв'язання задачі зводиться до формальних перетворень і призводить відразу до відповіді, яку залишається лише розшифрувати, виходячи з прийнятих вами позначень.

Табличний метод дуже наочний, але має універсальністю, тобто. призначений для вирішення лише одного типу завдань. Крім того, він вимагає аналізу інформації, що знаходиться в таблиці, вміння порівнювати ізіставляти.

Метод графів застосовується тоді, коли між об'єктами, про які йдеться у завданні, існує багато зв'язків. Граф дозволяє наочно уявити ці зв'язки та визначити, які з них не суперечать.

Метод діаграм Ейлера-Венна дозволяє графічно вирішувати математичні завдання з урахуванням застосування теорії множин.

Як правило, завдання можна вирішити декількома способами (методами). Щоб вибрати найпростіший і найефективніший спосіб кожної конкретної завдання, необхідно знати всі ці способи.

Розв'язання задач за допомогою алгебри висловлювань.

Щоб вирішувати завдання цим методом треба знати як основні логічні закони, а й вміти їх застосовувати, і навіть правильно складати тотожно істинні висловлювання.

В одній країні жили лицарі, які завжди говорили правду, тільки правду і нічого крім правди, і брехуни, які завжди брехали. Одного разу в країну проник шпигун на ім'я Мердок, який, як і всякий шпигун, іноді говорив правду, іноді брехав, залежно від того, що йому було вигідно. Шпигун оселився з двома жителями країни – лицарем та брехуном. Усіх трьох заарештували одного дня і привели на допит. Ніхто не знав хто з них хто. Вони зробили такі заяви: А сказав: Я -Мердок.У сказав:А говорить правду.

Хто ж із них шпигун - А, В чи С?

У наших позначеннях висловлювання А, В, С записуються так: А= Аш;В= Аш;С=&#175Cш .

За умов завдання ясно, що з трьох висловлювань істинним може бути або одне (якщо шпигун бреше), або два (якщо шпигун говорить правду). Отже, можливі такі варіанти розподілу істинних (І) і хибних (Л) висловлювань: <І>ІЛ V АБО V ЛІЇ VЛЛИ V ЛІЛ V ІЛЛ = 1. (*)

Подивимося, що означає ИИЛ для введених нами позначень.

Висловлювання бранця А істинно, отже, Аш= 1; висловлювання бранця істинно, отже, Аш=1; висловлювання бранця З помилково, отже, Сш=1. Тобто Аш& amp; # 38Аш& amp; Але А і С не можуть одночасно бути шпигунами, отже це невірно і дана кон'юнкція хибна.

Аналогічно варіант АБО "перекладається" в наші позначення так: Аш&#38&#175Аш&#38&#175Сш=1. Ця кон'юнкція теж хибна, оскільки А може одночасно бути шпигуном і бути ним.

Тобто ні А ні С не шпигуни, отже, шпигун В. далі вже просто зробити висновок, що А - брехун, С - лицар.

2. Розв'язання задач за допомогою кіл Ейлера.

Завдання, які можна вирішити за допомогою кіл Ейлера, не можна вирішити інакше, порівняно з табличним методом або за допомогою графів. Цей спосіб вирішувати завдання вигадав у XVIII ст. великий Леонард Ейлер. У цьому розділі курсової роботи я розгляну кілька завдань, які можна вирішити цим методом. Цей метод простий, якщо у ньому розібратись.

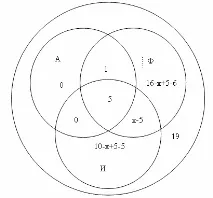
Зі співробітників фірми 16 побували у Франції,10-в Італії,6-в Англії; в Англії та Італії-5; в Англії та Франції -6; у всіх трьох країнах – 5 співробітників. Скільки людей відвідали і Італію, і Францію, якщо всього у фірмі працюють 19 осіб, і кожен із них побував хоча б в одній із цих країн?

Нам відомо, що у всіх трьох країнах було 5 працівників. В Англії та Італії теж 5, отже ці ж співробітники були і у Франції і тому у перетині кіл А та І ставимо 0. У Франції та Італії нам невідомо тому пишемо х-5 у перетині кіл А та Ф. Т.к. в Англії було 6 осіб, то6-5-1=0 пишемо 0, у Франції 16-х +5-6 та Італії 10-х +5-5 і всього у фірмі 19 співробітників, то залишається скласти і вирішити рівняння: 1+16-х +5-6+5+х-5+10-х+5-5=19, звідси х=7, отже в Італії та Франції побувало 7-5=2 співробітники фірми.

4. Розв'язання задач за допомогою графів.

Граф - одне із видів моделей, що відбивають взаємодія об'єктів чи систем.

Графом називають схему, в якій позначаються лише наявність об'єктів (елементів системи) та наявність та вид зв'язку між об'єктами.

Об'єкти представляються у графі вершинами (на схемі вони позначаються кружальцями, прямокутниками тощо). Зв'язки між об'єктами представляються, якщо зв'язок односпрямований (позначається на схемі лініями зі стрілками) або ребрами, якщо зв'язок між об'єктами двосторонній (позначається на схемі лініями без стрілок).

Наприклад, якщо потрібно подати у графі, що зі стану А в стан У можливий перехід під впливом V, то це можна зобразити так:

Якщо потрібно уявити, що к-тий учасник змагання зайняв n-е місце (або, що те саме, n-е місце зайняв к-тим учасником), це можна зобразити так:

Завдання N11.Марина, Лариса, Жанна та Катя вміють грати на різних інструментах (піаніно, віолончелі, гітарі, скрипці), але кожна тільки на одному. Вони ж знають іноземні мови (англійська, французька, німецька та іспанська), але кожна лише одна. Відомо:

1. Дівчина, яка грає на гітарі говорить іспанською.
2. Лариса не грає ні на скрипці ні на віолончелі та не знає англійської мови.
3. Марина не грає ні на скрипці, ні на віолончелі і не знає ні німецької, ні англійської.
4. Дівчина, яка розмовляє німецькою, не грає на віолончелі.
5. Жанна знає французьку мову,але не грає на скрипці.

Хто на якому інструменті грає та яку іноземну мову знає?

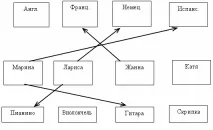
З п'ятої умови, що Жанна знає французьку мову, малюємо стрілку. З третьої умови, що Марина не знає ні німецької, ні англійської, а французька знає Жанна, то Марина знає іспанську і розглядаючи першу умову вона грає на гітарі. З умови N2 бачимо, що Лариса грає піаніно, т.к. Марина грає на гітарі, а на інших інструментах вона грати не вміє, і отже вона розмовляє німецькою.

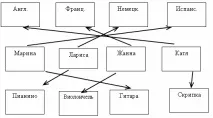
Т.к. Жанна не грає на скрипці, то залишається один інструмент, на якому вона може грати це віолончель. Тоді Катя грає на скрипці і знає англійську мову.

Мною були розглянуті різні методи розв'язання змістовних логічних завдань, це такі методи як метод вирішення задач за допомогою таблиці, за допомогою кіл Ейлера, за допомогою алгебри висловлювань і за допомогою графів. З цього можна дійти невтішного висновку, що, вирішуючи, якесь завдання не треба зупинятися на якомусь одному прийомі, адже найімовірніше це завдання можна вирішити й іншим методом, який буде і легше і простіше для даної задачі. Завдання, які я розібрала у своїй роботі, можна пропонувати і школярам і студентам вищих закладів. Я вважаю, що для школи тема моєї курсової роботи актуальна на додаткових заняттях з математики, а також для шкіл з поглибленим вивченням математики.

1. Цікава математика. 5 – 11 класи. (Як зробити уроки математики не нудними) / Авт.-сост. Т. Д. Гаврилова. – Волгоград: Вчитель, 2005. –96 с.
2. Ліхтарніков Л. М., Сукачова Т.Г. Математична логіка / Курс лекцій / Оформлення обкладинки О. Олексенко, С. Шапіро. - СПб.: Видавництво "Лань", 1998. - 288с.
3. Лискова В.Ю.,Ракітіна Є.А. Логіка в інформатиці. – М.: Лабораторія базових знань, 2001. – 160 с.: іл. Серія "Інформатика".

---