WolframAlpha по-українськи грудня 2012
Похідна, інтеграл, диференціальні рівняння та ряди онлайн з WolframAlpha ®
Математичні сніжинки у WolframAlpha

Зимові сніжинки мають безпосереднє відношення до математики: всі вони мають різноманітну, але характерну форму, яку дізнаєшся з першого погляду, і є гарною ілюстрацією геометричного поняття симетрії. До того ж, на сніжинки дуже зручно послатися, коли потрібно пояснити таке непросте поняття, як "фрактал".
З усього різноманіття відомих на сьогодні фрактальних ліній далі розглянемо лише їхні "новорічні" варіанти – "математичні сніжинки", які можна легко отримати за допомогою WolframAlpha.
Найбільш відомою з таких ліній є "сніжинка Коха" - одна з перших, досліджених вченими фракталів. Сніжинка Коха є класичним прикладом безперервної лінії, до якої не можна провести дотику в жодній точці. Вона має цілу низку дивовижних властивостей, і вперше була описана в статті шведського математика Хельге фон Коха (Niels Fabian Helge von Koch) у 1904 році: Ось, як вона виглядає:
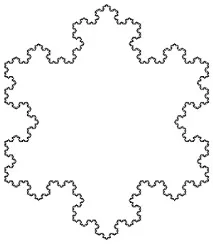
Дискретні імовірнісні розподіли у WolframAlpha

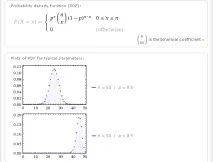
Після безперервних ймовірнісних розподілів розглянемо основні дискретні розподіли (discrete distributions). Найвідоміший з них - цебіноміальний розподілймовірностей:

Вище показанічислові характеристики біномного розподілу. А на наступній картинці - функція щільності ймовірностібіномного розподілу та типові графіки:
І, нарешті,функція біномного розподілута її типові графіки:
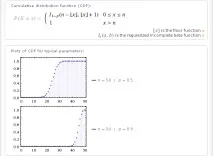
Аналогічні відомості за допомогою WolframAlpha можна отримати для наступних найбільш уживаних дискретних імовірнісних розподілів:
До речі, барвиста картинка на початку цієї посади отримана за допомогою WolframAlpha з використанням імовірнісних розподілів.
Безперервні імовірнісні розподіли у WolframAlpha
Імовірнісні розподіли грають виключно важливу роль у математиці, статистиці, математичному моделюванні, фізиці та ін. І в цьому питанні WolframAlpha як завжди поспішає нам на допомогу. Наприклад, якщо раптом Вам терміново знадобилася інформація про властивості ймовірнісного розподілу (properties of a continuous distribution), зверніться до WolframAlpha з відповідним запитом, і Ви відразу отримаєте потрібні відомості. Головне - це правильно поставити своє питання WolframAlpha, тобто правильно сформулювати потрібний запит.
У цій замітці Ви знайдете відповідь на питання, як за допомогою WolframAlpha отримати відповідь на питання, що стосуються властивостей основних імовірнісних розподілів безперервних випадкових величин.
У більшості випадків, щоб правильно звернутися до WolframAlpha за інформацією щодо ймовірнісних розподілів, потрібно згадати, як пишеться назва того чи іншого ймовірнісного розподілу англійською. Це стосується, перш за все, всього відомого нормального розподілу, який також називають розподілом Гауса.
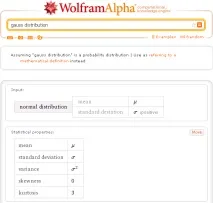
Основну інформацію щодо нормального розподілу, а саме - його властивості, графіки, числові характеристики - WolframAlpha виводить на запитnormal distribution(gauss distribution):
По-перше, на цей запит Ви отримаєте перелік основних числових характеристик нормального розподілу (normal distribution statistical properties):
Для всіх ймовірнісних розподілів WolframAlpha виводить п'ять основних числових характеристик:
- Mean – математичне очікування, середнє;
- Standard deviation – середньо-квадратичне відхилення;
- Variance – дисперсія;
- Skewness – асиметрія;
- Kurtosis – ексцес.

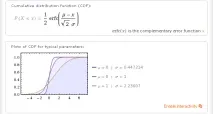
Нарешті, по-третє, WolframAlpha виводить деякі важливі перцентілі (percentiles) нормального розподілу:

Якщо Вам потрібно отримати окремі властивості безперервних ймовірнісних розподілів, то у своєму запиті перед назвою розподілу просто вкажіть потрібну Вам властивість. Наприклад, щоб отримати математичне очікування нормального розподілу, слід використати запит mean normal distribution. Щоб отримати щільність нормального розподілу, використовуйте запит pdf normal distribution. Запит cdf normal distribution виводить функцію нормального розподілу тощо. Будьте уважні - під час введення запитів використовуйте англійську розкладку клавіатури.
У наступних постах я збираюся показати докладніше, за допомогою яких запитів можна отримати окремі властивості ймовірнісних розподілів, як отримати властивості ймовірнісних розподілів із заданими параметрами, наведу список основних дискретних розподілів ймовірностей, а також покажу, якза допомогою WolframAlpha обчислюється ймовірність потрапляння випадкової величини заданий інтервал. До речі, останнє завдання з допомогою WolframAlpha вирішується однаково всім розподілів. Про це важливо знати, оскільки в університетських курсах (особливо на нематематичних факультетах університетів) це завдання розглядається, як правило, на рівні прикладу, та й лише для нормального розподілу безперервних випадкових величин, а також для біноміального розподілу дискретних випадкових величин.