Різні геометричні завдання
У цій статті ми розглянемо рішення різних завдань, які здалися мені нетривіальними, цікавими, із родзинкою.
1. У трапецію АВСD, бічні сторони якої СD і AB рівні відповідно 6 і 10, вписано коло радіуса 3. Продовження бічних сторін перетинаються в точці М. Потрібно знайти радіус кола, описаного біля трикутника AMD.

Діаметр вписаної в трапецію кола дорівнює 6. Так як вписане коло стосується основ трапеції, то її діаметр є висотою нашої трапеції. Але бічний бік її теж 6! Відомо, що перпендикуляр – найкоротша відстань між будь-якими об'єктами, тому бічна сторона СD – перпендикулярна основам трапеції, інакше вона була б більшою довжиною. Таким чином, трапеція прямокутна і трикутник ADM теж прямокутний. Тоді, щоб знайти радіус описаного біля нього кола, потрібно знайти його гіпотенузу – радіус, що шукається, дорівнюватиме її половині.
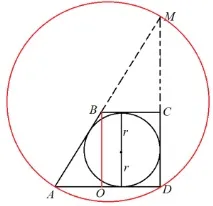
Розглянемо тепер малюнок праворуч: проведемо висоту трапеції з вершини, як це показано червоною лінією малюнку. У трикутнику АОВ відомі гіпотенуза (10) та висота (6). Визначимо його основу АТ з теоремі Піфагора – це другий його катет, і він дорівнює 8:
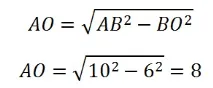
Тепер можемо визначити основи нашої трапеції. Якщо чотирикутник вписано коло, то такий чотирикутник є описаним, і за властивістю описаного чотирикутника суми його протилежних сторін рівні. Тобто сума підстав дорівнює сумі бічних сторін, BC+AD=16. Тоді, оскільки OD=BC, то
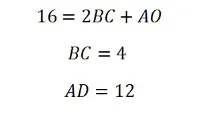
Знаючи основу трикутника AMD, можемо знайти його гіпотенузу. Тут можна скористатися подобою трикутників ABO та AMD, а можна – теоремою синусів. Також можна визначитикосинус кута А, і потім, знаючи його, знайти гіпотенузу трикутника AMD:
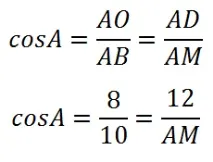
Отже, АМ=15. Радіус описаної біля трикутника АMD кола тоді 7.5
2. Площина, що перетинає вісь циліндра, перетинає основи циліндра по хордах, довжини яких дорівнюють 6 і 8. Знайдіть тангенс кута між цією площиною і площиною основи циліндра, якщо діаметр основи дорівнює 10, а утворює 14.
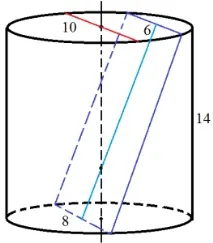
Намалюємо креслення: Щоб визначити тангенс шуканого кута (малюнок праворуч), необхідно знайти тільки відстань між хордами.
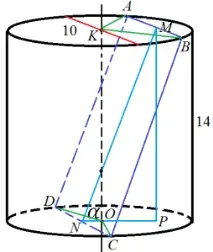
Ця відстань – прилеглий катет трикутника MNP, тангенс кута N якого ми шукаємо. Протилежний катет – циліндра, що утворює, і вона нам відома. Тобто нам достатньо знайти відстані KM та NO і скласти їх. КM – висота рівнобедреного трикутника ABK. NO – висота рівнобедреного трикутника DOC. Рівностегнові вони тому, що їхні бічні сторони – радіуси циліндра. Знайдемо площі цих трикутників за формулою Герона, тоді ми зможемо дізнатися про їхні висоти. Формула Герона:
Тут p – напівпериметр трикутника. Тоді:

Оскільки основа трикутника AKB дорівнює 6 (це відома нам хорда), його висота, очевидно, дорівнює 4. Отже, KM=4.
Тепер розглянемо трикутник DNC:

Оскільки основа трикутника DNC дорівнює 8 (це друга відома нам хорда), його висота, очевидно, дорівнює 3, ON=3. Отже, NP=NO+KM=7.
Тоді тангенс шуканого кута можна визначити з прямокутного трикутника NPM:
Відповідь: тангенс кута дорівнює 2.
3. Площина перетинає дві кулі, що мають загальний центр. Площа перерізу меншої кулі цією площиною дорівнює 7. Площина, паралельна, стосується меншої кулі, а площа перерізу більшої кулі цією площиною дорівнює 5.Знайдіть площу перерізу більшої кулі площиною.
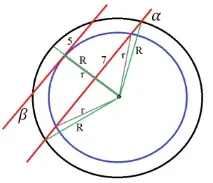
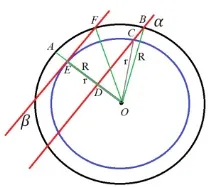
Побудови задачі 3
Червоними лініями показані площини, що січать кулі. Зелені лінії – радіуси більшої кулі, сірі – меншої. Розставимо літери, щоб позначити необхідні відстані:
Щоб визначити площу перерізу (яка є коло), необхідно знати радіус цього кола. Нам потрібно знайти довжину відрізка DB. Цей відрізок є катетом прямокутного трикутника DOB. Прямокутний він тому, що площина за умовою стосується меншої кулі, отже, відрізок EO перпендикулярний їй, і, отже, перпендикулярний і площині, якщо площини паралельні. У трикутнику DOB відома довжина гіпотенузи BO – це радіус більшої кулі R. Таким чином, потрібно знайти DO, щоб скористатися теоремою Піфагора.
Розглянемо трикутник EFO. Його гіпотенуза – це також R, а один із катетів – EO – це радіус меншої кулі r. Тоді
Зауважимо, що відома нам площа, рівна за умовою 5.
У трикутнику DOC:
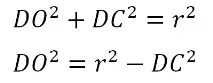
З трикутника DBO висловимо шуканий радіус DB:
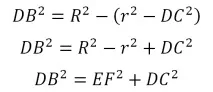
Тут теж фігурує величина відома: - площа, рівна за умовою 7. Помножимо останнє рівняння на , і ось вона - площу перерізу, що шукається!
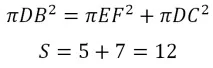
4. Знайдіть об'єм і площу поверхні тіла, отриманого при обертанні трикутника зі сторонами 13, 14 і 15 навколо прямої, що проходить через вершину середнього за величиною кута трикутника паралельно до середньої його сторони.
Щоб краще уявити, як може виглядати подібна фігура, розглянемо креслення:
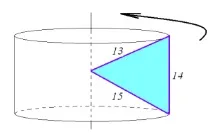
Середній кут трикутника лежить проти його середньої сторони - тобто це кут, що протилежить стороні з довжиною 14. Тоді при обертаннітрикутника вийде циліндр, з якого "вирізані" два конуси: зверху та знизу. Висота нашого циліндра дорівнює довжині сторони – 14, а утворюючі конусів дорівнюють 13 і 15. Тоді об'єм такої фігури дорівнює об'єму циліндра за вирахуванням об'ємів двох конусів, а площа поверхні – це сума бічних поверхонь обох конусів та циліндра.
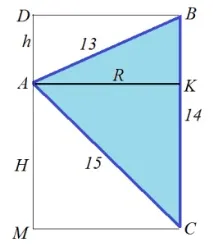
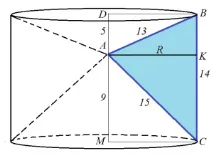
Тут представлено осьовий переріз циліндра (вірніше, його половина). Цей малюнок допоможе визначити радіус циліндра R. Видно, що радіус циліндра, що шукається, - це висота трикутника ABC - AK. Щоб визначити висоту, знайдемо площу трикутника ABC. Тут можна скористатися формулою Герона:
Знайдемо половину периметра:
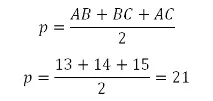
Тепер визначимо площу:
Знаючи площу трикутника, просто знайти висоту, а в нашому випадку це радіус циліндра:
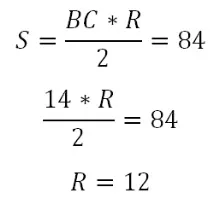
Визначимо тепер висоти конусів h і H. Це можна зробити за теоремою Піфагора із трикутників ABD та ACM:
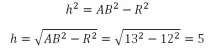
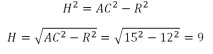
Тепер нам відомі радіус циліндра, що утворюють і висоти конусів, так що знайти необхідний об'єм та площу поверхні – справа техніки, як кажуть:
Визначення повної поверхні
Площа бічної поверхні циліндра:
Площа бічної поверхні конуса з меншою висотою:
Площа бічної поверхні конуса з більшою висотою:
Загальна площа поверхні:
Об'єм меншого конуса:
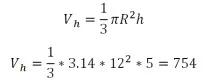
Об'єм більшого конуса:
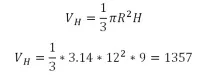
Об'єм фігури, що шукається, дорівнює різниці об'ємів циліндра і двох конусів: