Місткові схеми - Студопедія
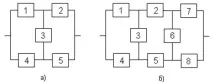
Місткова структура (рис. 2, а, б) не зводиться до паралельного або послідовного типу з'єднання елементів, а являє собою паралельне з'єднання послідовних ланцюжків елементів з діагональними елементами, включеними між вузлами різних паралельних гілок (елемент 3 на рис. 2, а елементи 3 та 6 на рис.2, б). Працездатність такої системи визначається не тільки кількістю елементів, що відмовили, але і їх становищем у структурній схемі. Наприклад, працездатність ТЗ, схема якої наведена на рис. 2, а буде втрачена при одночасному відмові елементів 1 і 2, або 4 і 5, або 2, 3 і 4 і т.д.. У той же час відмова елементів 1 і 5, або 2 і 4, або 1, 3 і 4, або 2, 3 та 5 до відмови системи не призводить.
| Малюнок 2. Місткові схеми |
Імовірність безвідмовної роботи системи визначається як сума ймовірностей усіх працездатних станів:
(27)
У разі рівнонадійних елементів
(28)
Метод прямого перебору ефективний лише за малої кількості елементів n, оскільки кількість станів системи становить . Наприклад, для схеми на рис. 2,б їх кількість становитиме вже 256. Деяке спрощення досягається, якщо таблицю станів включати лише поєднання, відповідальні працездатному (чи лише непрацездатному) стану системи загалом.
Для аналізу надійності ТЗ, структурні схеми яких не зводяться до паралельного або послідовного типу, можна скористатися також методом логічних схем із застосуванням логіки алгебри (бульової алгебри). Застосування цього зводиться до складання для ТЗ формули алгебри логіки, що визначає умова працездатності системи. При цьому для кожного елемента та системи в ціломурозглядаються дві протилежні події - відмова та збереження працездатності.
Для складання логічної схеми можна скористатися двома методами – мінімальних шляхів та мінімальних перерізів.
Розглянемо метод мінімальних шляхів до розрахунку ймовірності безвідмовної роботи з прикладі місткової схеми (рис. 2,а).
Мінімальним шляхом називається послідовний набір працездатних елементів системи, який забезпечує її працездатність, а відмова будь-якого з них призводить до її відмови.
Мінімальних шляхів у системі може бути один чи кілька. Очевидно, що система з послідовним з'єднанням елементів (рис. 1) має тільки один мінімальний шлях, що включає всі елементи. У системі з паралельним з'єднанням (рис. 2) кількість мінімальних шляхів збігається з числом елементів і кожен шлях включає один з них.
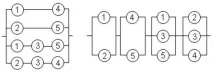
Для місткової системи з п'яти елементів (рис. 2,а) мінімальних шляхів чотири: (елементи 1 та 4), (2 та 5), (1, 3 та 5), (2, 3 та 5). Логічна схема такої системи (рис. 3) складається таким чином, щоб усі елементи кожного мінімального шляху були з'єднані один з одним послідовно, а всі мінімальні шляхи паралельно.
| Рисунок 4 Логічна схема місткової системи за методом мінімальних перерізів |
| Рисунок 3 Логічна схема місткової системи за методом мінімальних шляхів |
Потім для логічної схеми складається функція алгебри логіки А за загальними правилами розрахунку ймовірності безвідмовної роботи, але замість символів ймовірностей безвідмовної роботи елементівpiі системи Р використовуються символи події (збереження працездатності елементаaiі системи А). Так, "відмова" логічної схеми рис. 3 полягає водночасної відмові всіх чотирьох паралельних гілок, а "безвідмовна робота" кожної гілки - в одночасній безвідмовній роботі її елементів. Послідовна сполука елементів логічної схеми відповідає логічному множенню (“І”), паралельне - логічному додаванню (“АБО”). Отже, схема рис. 3.3 відповідає затвердженню: система працездатна, якщо працездатні елементи 1 і 4, або 2 і 5, або 1,3 та 5, або 2,3 та 4. Функція алгебри логіки запишеться:
(29)
У виразі (29) змінні ж розглядаються як булеви, тобто. можуть прийматись лише два значення: 0 або 1. Тоді при зведенні в будь-який ступінь k будь-яка змінна a зберігає своє значення: . На основі цієї властивості функція алгебри логіки (29) може бути перетворена на вигляд
(30)
Замінивши у виразі (30) символи подій їх ймовірностями отримаємо рівняння для визначення ймовірності безвідмовної роботи системи
(31)
Для системи рівнонадійних елементів вираз (31) легко перетворюється на формулу (28).
p align="justify"> Метод мінімальних шляхів дає точне значення тільки для порівняно простих систем з невеликим числом елементів. Для складніших систем результат розрахунку є нижньою межею ймовірності безвідмовної роботи.
Для розрахунку верхньої межі ймовірності безвідмовної роботи системи є метод мінімальних перерізів.
Мінімальним перетином називається набір непрацездатних елементів, відмова яких призводить до відмови системи, а відновлення працездатності будь-якого з них - відновлення працездатності системи. Як і мінімальних шляхів, мінімальних перерізів може бути кілька. Очевидно, що система з паралельним з'єднанням елементів має тільки один мінімальний переріз, що включає всі її елементи (відновлення будь-якоговідновить працездатність системи). У системі з послідовним з'єднанням елементів число мінімальних шляхів збігається з числом елементів, і кожен переріз включає один із них.
У містковій системі (рис. 2 а) мінімальних перерізів чотири (елементи 1 і 2), (4 і 5), (1, 3 і 5) , (2, 3 і 4). Логічна схема системи (рис.4) складається таким чином, щоб усі елементи кожного мінімального перерізу були з'єднані один з одним паралельно, проте мінімальні перерізи - послідовно. Аналогічно методу мінімальних шляхів складається функція алгебри логіки. "Безвідмовна робота" логічної системи рис. 4 полягає у "безвідмовній роботі" всіх послідовних ділянок, а "відмова" кожного з них - в одночасному "відмові" всіх паралельно включених елементів. Як бачимо, оскільки схема методу мінімальних перерізів формулює умови відмови системи, у ній послідовне з'єднання відповідає логічного “АБО”, а паралельне - логічного “І”. Схема рис. 4 відповідає формулюванню: система відмовить, якщо відмовить елементи 1 і 2, або 4 і 5, або 1, 3 і 5, або 2, 3 і 4. Функція логіки алгебри запишеться
(32)
Після перетворень з використанням властивостей булевих змінних (32) набуває форми (30), після заміни подій їх ймовірностями перетворюється на вираз (31).
Таким чином, для місткової системи з п'яти елементів верхня та нижня межі ймовірності безвідмовної роботи, отримані методами мінімальних перерізів та мінімальних шляхів, збіглися з точними значеннями (28), отриманими методом прямого перебору. Для складних систем це може не статися, тому методи мінімальних шляхів та мінімальних перерізів слід застосовувати спільно.
У ряді випадків аналізу надійності ТЗ вдається скористатися методом розкладання щодоособливого елемента, заснованими на відомій у математичній логіці теоремі про розкладання функції логіки за будь-яким аргументом. Відповідно до неї, можна записати:
(33)
де і - ймовірності безвідмовної роботи та відмови i - го елемента, і - ймовірності працездатного стану системи за умови, що i - елемент абсолютно надійний і що i - елемент відмовив.
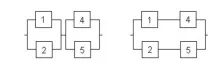
Для місткової схеми (рис. 2, а) в якості особливого елемента доцільно вибрати діагональний елемент 3. При місткова схема перетворюється на паралельно - послідовне з'єднання (рис. 5, а), а при - в послідовно - паралельне (рис. 5, б ).
| Малюнок 5. Перетворення місткової схеми при абсолютно надійному (а) і центральному елементі, що відмовив (б) |
Для перетворених схем можна записати:
(34)
(35)
Тоді на підставі формули (33) отримаємо:
(36)
Легко переконатися, що для рівнонадійних елементів формула (36) перетворюється на (28).
Цим методом можна і при розкладанні щодо кількох “особливих” елементів. Наприклад, для двох елементів (i, j) вираз (33) набуде вигляду:
(37)
Імовірність безвідмовної роботи місткової схеми (рис. 2 б) при розкладанні щодо діагональних елементів 3 і 6 по (37) визначиться:
(38)
Імовірності легко ставити, виконавши попередньо перетворені схеми, подібно до рис. 5 а, б.
Чи не знайшли те, що шукали? Скористайтеся пошуком:
Вимкніть adBlock! і оновіть сторінку (F5)дуже потрібно