Алгебраїчна теорія графів
Алгебраїчна теорія графів- це галузь математики, в якій застосовуються методи алгебри до завдань з графами. Інші підходи до завдань із графами - це геометричний [en] , комбінаторний та алгоритмічний. Існує три основні гілки алгебраїчної теорії графів - дві гілки використовують лінійну алгебру та теорію груп, а одна гілка вивчає інваріанти графа.
Зміст
Використовують лінійну алгебру
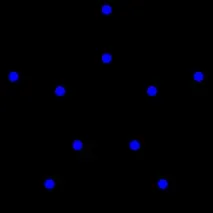
Перша гілка алгебраїчної теорії графів вивчає графи з допомогою лінійної алгебри. Особливо в ній вивчаються спектри матриці суміжності або матриці Кірхгофа графа (ця частина алгебраїчної теорії графів називається також спектральною теорією графів). Для графа Петерсена, наприклад, спектр суміжної матриці дорівнює (-2, -2, -2, -2, 1, 1, 1, 1, 1, 3). Деякі теореми пов'язують властивості спектра коїться з іншими інваріантами графа. Як простий приклад, зв'язковий граф з діаметромDматиме щонайменшеD+1 різних значень у своєму спектрі [1] . Властивості спектра графа використовуються для аналізу синхронізації мереж [en] .
Використовують теорію груп
Ця друга гілка алгебраїчної теорії графів пов'язана з першою, оскільки властивості симетрії графа відображаються у його спектрі. Зокрема спектр графа з високою симетрією, такого як граф Петерсена, має мало різних власних значень [1] (у графа Петерсена 3 значення, що є мінімальним можливим числом для такого графа з діаметром, як у графа Петерсена). Для графів Келі спектр може бути пов'язаний прямо зі структурою групи, зокрема, з її неприведеними уявленнями [1] [3] .
Вивчення інваріантів графа
Нарешті, третя гілка алгебраїчної теорії графів працює з властивостями алгебриінваріантів графів, зокрема з хроматичними багаточленами, багаточленами Татта [en] та інваріантами вузлів. Хроматичний багаточлен графа, наприклад, підраховує кількість його правильних забарвлень вершин. Для графа Петерсена цей багаточлен дорівнює t(t−1)(t−2) 67t^-230t^+529t^-814t^+775t-352)> [1] . Зокрема, це означає, що граф Петерсена не можна правильно розфарбувати одним або двома кольорами, але трьома кольорами його можна розфарбувати 120 різними способами. Багато робіт у цій галузі алгебраїчної теорії графів було викликано спробами довести теорему про чотири фарби. Однак залишається багато відкритих питань, таких як визначення графів, що мають той самий хроматичний багаточлен, і визначення, які є хроматичними.