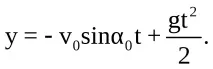§5. Вільне падіння по вертикалі
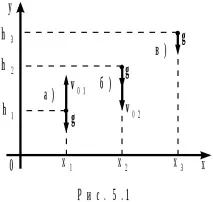
Вільне падіння матеріальної точки біля поверхні Землі- рівнозмінний рух, що відбувається при малих висотах h (h 2 ).
Рух матеріальної точки біля Землі по вертикалі є рівнозмінним прямолінійним рухом у системі відліку, що з поверхнею Землі, у випадках, коли м.т. кидають вертикально вгору (рис.5.1,а) або вниз (рис.5.1,б) з деякою початковою швидкістю (можливо, з деякою висоти) або коли м.т. падає вниз без початкової швидкості (рис.5.1, в) з деякою висоти.
П
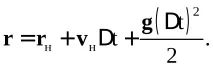
Рівнянням (5.1) та (5.2) еквівалентні такі системи рівнянь (tн = 0):
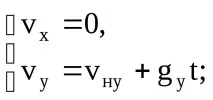
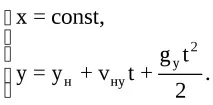
Відповідно до цих рівнянь, проекція швидкості матеріальних точок на вісь Oy у системі відліку, показаної на рис.5.1, дорівнює:
y-координата матеріальних точок дорівнює:
1-ий
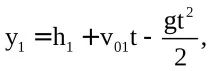
Другий
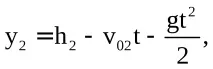
3-ї
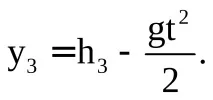
Вирішуючи, наприклад, рівняння (5.8) щодо часу t, можна визначити моменти часу, у яких м.т. знаходиться на висоті h (наприклад, коли h більше початкової висоти h1), а потім визначити проекцію та модуль швидкості на цій висоті під час руху м.т. вгору або вниз за допомогою рівняння (5.5).
§6. Рух під кутом до горизонту
Д
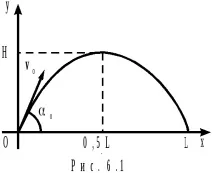
При такому русі:
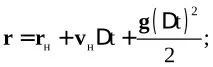
(6.3)
(6.4)
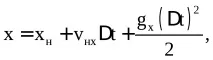
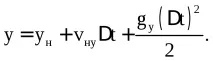
При визначенні проекцій швидкості та прискорення на осі координат Ох та Оу,показаних на рис.6.1, та їх підстановки рівняння (6.3) – (6.6) виходять рівності (при хн = 0, ун = 0, tн = 0)для проекцій швидкості:
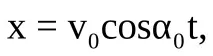
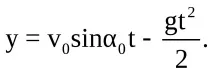
Вирішуючи спільно рівності (6.7) (6.10), можна визначити:
час підйому на максимальну висоту
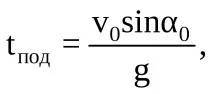
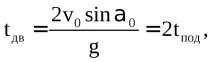
максимальну висоту підйому
ymax =
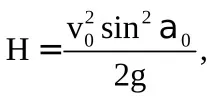
максимальну дальність польоту
xmax =
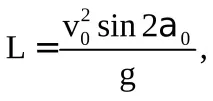
рівняння траєкторії (при русі м.т. у площині хОу)
(6.15)
(траєкторією м.т. є парабола, представлена на рис.6.1),
залежність проекції швидкості на вісь Oy від висоти h:
(6.16)
(6.17)
модуля швидкості від висоти
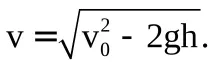
При виборі іншої системи координат, що відрізняється від системи, показаної на рис.6.1, рівняння (6.3) - (6.6) не змінюються, деякі (або всі) рівняння (6.7) - (6.10) зміняться. Так, наприклад, якщо вісь Оу буде спрямована вертикально вниз (напрямок осі Ох не змінюється), то